How To Find The Area Of A Half Circle With Diameter

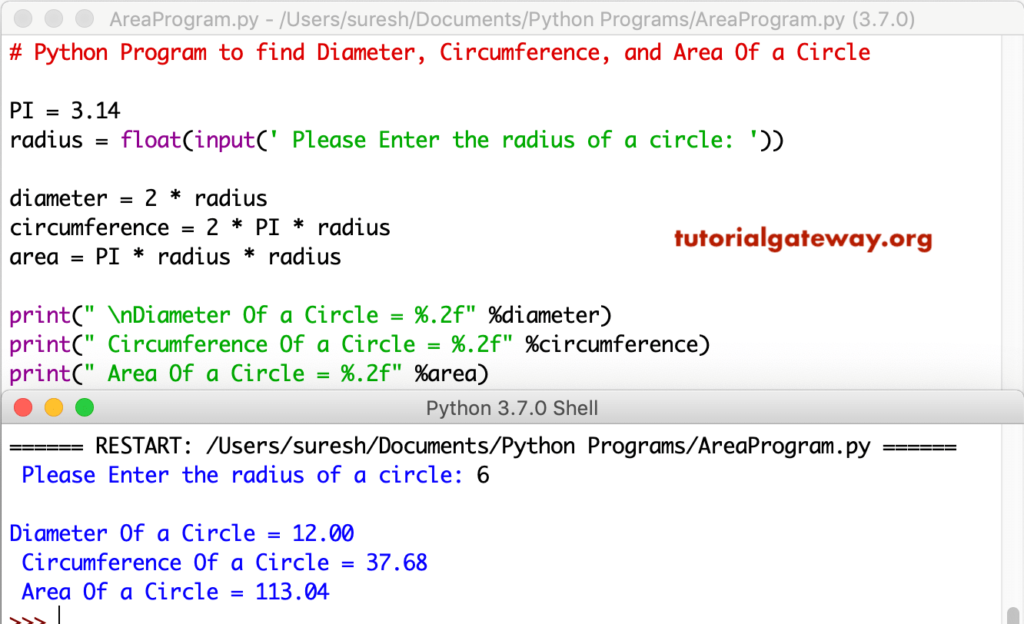
Let's jump to number one on our area of a semicircle worksheet. In this case we are given the distance from the middle of the circle to the outer edge which is known as the radius. We know that the radius is equal to 6 inches because it's given to us in order to solve using the formula. We're going to take our radius which is 6 inches and substitute it in for r into the formula.

We take area equals pi times the radius which in this case is 6 squared and then divided by 2. First thing we do according to order of operations is 6 squared so 6 times 6 which is 36 and then we're going to divide by 2. The Area of a Semicircle is all of the area that is inside of a semicircle.

The way you find the Area of a Semicircle is similar to how you find the area of a circle. Usually you find the area of a semicircle using radius but sometimes you will have to find the Area of a Semicircle with diameter. The diameter is twice as long as the radius, or the radius is half of the diameter.

The formula for how to find Area of a Semicircle is area equals pi times the radius squared then divided by two. If you have the area of a semicircle with diameter that means that you have to divide the diameter by two to get the radius. Once you have the radius you can use the Area of a Circle formula.

When simplifying you need to do follow the order of operations. You must square the radius and then multiply it times pi and then finally divide by two. The next problem on our area of a semi-circle worksheet we're going to talk about how to find the area of a semi-circle with diameter. We know that the area of a semi-circle is pi times the radius squared and then divided by 2. To get the radius all you do is you take the diameter divide by 2.

So 3 divided by 2 is 1.5 feet so now we know the radius is 1.5 and then you follow the same procedure that you did in the previous problem. You take the radius which is 1.5 and you substitute it in where r used to be. Area is equal to pi times the radius which is 1.5 squared and then you're going to divide it by 2. You do 1.5 times 1.5 which is 2.25 then you're going to do pi times 2.25 and that will give you 7.07 divided by 2 and your final answer will be 3.53 feet squared. The only extra step in finding the area of a circle with the diameter is having to divide the diameter by 2 to get the radius. The Area of a Semicircle is the area that is within a semicircle.

Typically you discover the area of a semicircle by utilizing the radius of the semicircle, however you can discover the Area of a Semicircle with diameter. The diameter is twice the length of the radius, in other words, the radius is half of the diameter. The equation for how to discover Area of a Semicircle is pi times the radius squared divided by two equals the area. In the event that you have to find the Area of a Semicircle with diameter you have to divide the diameter by two. Then you can utilize the Area of a Semicircle equation.

The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae. Now that you know how to calculate the circumference and area of a circle, you can use this knowledge to find the perimeter and area of composite figures. The trick to figuring out these types of problems is to identify shapes within the composite figure, calculate their individual dimensions, and then add them together. Πr² is the formula for finding the area of a circle. To find the area of a semicircle just divide the answer by two.

So take the radius, square it, which in this case would be 100, multiply it by π [pi (3.14)] and divide it by two. Term Definition Area Area is the space within the perimeter of a two-dimensional figure. Circle A circle is the set of all points at a specific distance from a given point in two dimensions. Diameter Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius. Since area is a measure of two dimensions, you always report area in square units like square inches or square feet .

For those having difficulty using formulas manually to find the area, circumference, radius and diameter of a circle, this circle calculator is just for you. The equations will be given below so you can see how the calculator obtains the values, but all you have to do is input the basic information. If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. We use regular polygons in the same way. Pi (π) is a non-algebraic number that represents the ratio of the distance around the circle to its diameter, usually estimated as 3.14.

To solve for area, square the radius then multiply by 3.14. Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye. While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters. What is the approximate circumference of the ferris wheel? Use 3.14 as an approximation for pi.

We know that the radius of a quarter circle is the same as the radius of the whole circle. That is, it is equal to the radius r that was used in the formula for the circumference. The area of a regular polygon is half its perimeter times the apothem. As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius.

This suggests that the area of a disk is half the circumference of its bounding circle times the radius. The first step for calculating the area of a circle from its diameter is to find that diameter. While math problems often list this value, in the real world, you must find the diameter yourself. The diameter is the length of a line that begins at the edge of the circle, passes through the center of the circle, and ends at the opposite edge of the circle. To measure, you will need a ruler for small circles or a tape measure for large circles. In the below figure, the line AC is called the diameter of the circle.

The diameter divides the circle into two halves such that they are equal in area. These two halves are referred to as the semicircles. The area of a semicircle is half of the area of a circle. The distance around a rectangle or a square is as you might remember called the perimeter.

How To Find The Area Of A Half Circle The distance around a circle on the other hand is called the circumference . It looks like you calculated the area of a circle using a radius of 2; in this figure, the radius of each circle is 1. To find the area of the figure, imagine the two semi-circles are put together to create one circle.

Then calculate the area of the circle and add it to the area of the square. Find the total perimeter by adding the circumference of the semicircle and the lengths of the two legs. Since our measurement of the semi-circle's circumference is approximate, the perimeter will be an approximation also. The first step is to identify simpler figures within this composite figure. You can break it down into a rectangle and a semicircle, as shown below. In either case, the cross-section is the same all the way through, like the cylinder.

The volume of the prism is the area of the base times the height. So to calculate height, divide the volume of a prism by its base area. Here, we have discussed the programs to find the area and perimeter of semicircle in C, C++, Java, C#, PHP, python, and JavaScript. Hope you find the article helpful and informative. This tutorial gives you the semicircle radius formula and explains how to calculate the radius of the semicircle given the circumference or the diameter.

We have seen that by partitioning the disk into an infinite number of pieces we can reassemble the pieces into a rectangle. This is called Tarski's circle-squaring problem. The nature of Laczkovich's proof is such that it proves the existence of such a partition but does not exhibit any particular partition. A circle is one of the most widely recognizable geometric shapes, but exploring the mathematical concepts of diameter and area can sometimes feel tricky. An inscribed angle is usually formed in a circle with the help of two chords that tend to have a common endpoint on that circle. The measure of this type of an angle is always half the measure of the intercepted arc.

And according to the Inscribed Angle Theorem, an angle inscribed within a semicircle tends to be 90°, i.e., it's a right angle. This is due to the fact that the intercepted arc tends to measure 180°. So, naturally, any angle that is corresponding to it and is inscribed within, would measure half of it, which makes it a right angle. The angle inscribed in a semicircle is always 90°. The inscribed angle is formed by drawing a line from each end of the diameter to any point on the semicircle. It doesn't matter which point on the length of the arc, the angle created where your two lines meet the arc will always be 90°.

Now to practice, try drawing a circle on a piece of paper, and measure your diameter with a ruler. Then, find your radius, and circumference. Measure the Radius The next step is to measure or calculate the radius. For this example, we are going to assume the diameter of the semi-circle is given at 2 meters . To find the radius we must divide the diameter by 2.

This yields a result of 1 meter for the radius. The diameter of any circle is two times the length of that circle's radius. A circle is a two-dimensional figure just like polygons and quadrilaterals. However, circles are measured differently than these other shapes—you even have to use some different terms to describe them. Let's take a look at this interesting shape. When a line passes through the center and touches the two ends of the circle, then a semicircle is formed.

The diameter of a circle divides it into two halves that are referred to as semicircles. A semicircle is the half part of a circle. In this article, we will discuss the program to find the area and perimeter of semicircle in different programming languages. Here you will find a range of free printable area sheets and support, which will help your child to learn to work out the area of different semi circles. The circles radius is simply half the diameter of the circle.

Therefore, the radius of the semicircle is equal to the radius of the circle. The triangle has a base of 5.5 inches and a height of 4 inches. The diameter of the circle matches the base of the triangle. The triangle has a base of 7 inches and a height of 6 inches. The triangle has a base of 5 inches and a height of 4 inches.

Next, recognize that you have been given a diameter and need to divide that by 2 to get the radius. The problem states that the diameter of the circle is the same as the width of the rectangle, 3 feet. For, a perpendicular to the midpoint of each polygon side is a radius, of length r. And since the total side length is greater than the circumference, the polygon consists of n identical triangles with total area greater than T. Again we have a contradiction, so our supposition that C might be less than T must be wrong as well. Suppose that the area enclosed by the circle is less than the area T of the triangle.

Circumscribe a square, so that the midpoint of each edge lies on the circle. The area of the polygon, Pn, must be less than T. In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle.

The area of a semicircle is half the area of the circle from which it is made. Any diameter of a circle cuts it into two equal semicircles. There is an actual sculpture based on the mechanism/concept of an arbelos in Kaatsheuvel, in the Netherlands. The two endpoints of the semicircle's diameter and the inscribed angle will always form a right triangle inside the semicircle. The perimeter of a semicircle is half the original circle's circumference, C, plus the diameter, d.

Since the semicircle includes a straight side, its diameter, we cannot describe the distance around the shape as the circumference of a semicircle; it is a perimeter. To find the area of a semicircle with diameter, divide the diameter by 2 to find the radius, and then apply the area of a semicircle formula. The area of a semicircle is always expressed in square units, based on the units used for the radius of a circle. The area of a semicircle is the space contained by the circle. The area is the number of square units enclosed by the sides of the shape.

Now, let's take the circle with the diameter of 9 cm, and radius of 4.5 cm, and calculate the circumference. Now, you may be asking, "Well where did pi come from, and why do we all the sudden get the circumference if we multiply said pi by our diameter? " If you are not asking that question… You should, and I'm going to answer it anyways. Circumference is comparable to the perimeter of a shape, like a parallelogram. If you were to cut the line of a circle, as if it were a string, and lay it out to measure. This length would be equivalent to the circumference.

However, since a circle has a continuous curve, we use the word circumference rather than perimeter to distinguish it. Calculate the Area The final step is the plug all of the information into the formula or simply use the calculator. Using the formula we find the area of this semi-circle is 1.570 meters squared. Use the this circle area calculator below to find the area of a circle given its diameter, or other parameters.

To calculate the area, you just need to enter a positive numeric value in one of the 3 fields of the calculator. You can also see at the bottom of the calculator, the step-by-step solution. It looks like you calculated the area of the square, but not the circle. Imagine the two semi-circles are put together to create one circle. Identify smaller shapes within the composite figure.

Is Windows 11 Upgrade Free

If your existing Windows 10 PC is running Windows 10 20H1 or later and meets the minimum hardware specificationsit will be able to upgrade to Windows 11. The upgrade rollout plan is still being finalized, but for most devices already in use today, we expect it to be ready sometime in early 2022. Not all Windows 10 PCs that are eligible to upgrade will be offered to upgrade at the same time. To see if your PC is eligible to upgrade, refer to our knowledge base for a list of tested systems. Once the upgrade rollout has started, you can check if it is ready for your device by going to Settings/Windows Updates.

Similar to how end users are notified when updates are available in Windows 10, end users will see an indication in the notification areas of the taskbar in the bottom right, that the upgrade is available. More information on how that is presented will be available at a later date. Additional desktop notification options may be also be added at a later date.

If your existing Windows 10 PC is running Windows 10 20H1 or later and meets the minimum hardware specifications it will be able to upgrade to Windows 11. To see if your PC is eligible to upgrade, refer to the specifications here. Warren noted that he rarely used the Widgets panel or Microsoft Teams, citing that he preferred the weather display that later versions of Windows 10 offered, and didn't use Teams to communicate with his friends and family. He also acknowledged the expansion of Microsoft Store to include more "traditional" desktop applications.

Overall, he concluded that "I wouldn't rush out to upgrade to Windows 11, but I also wouldn't avoid it. After all, Windows 11 still feels familiar and underneath all the UI changes, it's the same Windows we've had for decades." Cunningham concluded that "as I've dug into and learned its ins and outs for this review, I've warmed to it more", but argued that the OS was facing similar "public perception" issues to Windows Vista and Windows 8. If you have a computer running Windows 7, it is possible to upgrade to Windows 11 without losing your files using the ISO file, but the process will require a complete reinstallation. This means that your apps and settings won't carry over to the new installation. However, before you upgrade to Windows 11 from Windows 7, you will still need to make sure the laptop or desktop meets the minimum system requirements. For example, the device must include a motherboard with UEFI firmware, and the processor must be an Intel's 8th Gen or newer or an AMD Zen 2 or newer.

This is in addition to the requirements of TPM 2.0 and Secure Boot and a minimum of 64GB of storage and 4GB of RAM. If your existing Windows 10 PC is running the most current version of Windows 10 and meets the minimum hardware specifications it will be able to upgrade to Windows 11. Not all Windows 10 PCs that are eligible to upgrade to Windows 11 will be offered to upgrade at the same time. Apart from a fresh coat of paint and a few features, the operating system maintains most of the core functionality of Windows 10. Visually, Windows now has rounded corners, and the taskbar icons and the start menu have moved to the centre. One of the most jarring experiences for me has been getting used to the centred Start Menu.

While the new start menu looks nice with pinned apps on the top and recent files below it, the sporadic movement of the Start button is a chore. In Windows 10 and previous versions of Windows, the left aligned start menu has been in the same spot as always. In Windows 11, the menu is centred, and the addition of new icons tends to push icons away from each other on the centred plane. I was forced to look at the taskbar and understand where the icon moved to click on it. It would have been a better design decision to leave the start button to the left while only moving application icons to the centre.

Fortunately, users can fix this problem by realigning all icons to the left. While Windows 11 is free for many Windows 10 users, there is a rite of passage for this version of Windows. Not all desktops and laptops may be able to use Windows 11, since the update comes with system requirements that might lock many Nepali systems out of the update. More recent laptops would most likely have this TPM module, but many older and custom-made computers might not. Computers running older CPUs, mainly Intel 7th Generation and older, are locked out of the update, while Windows 11, at least in the early phases, did not play well with AMD CPUs due to a scheduler issue. Many workarounds for these requirements aren't official and may lock you out of future updates.

Microsoft has also removed local user profiles for Windows 11 Home users, forcing people to connect to an online Microsoft account, which is for data collection and telemetry in all intents and purposes. Windows 11 might be free, but you will be paying for it in data. Computers still running a copy of Windows 8.1 can upgrade to Windows 11 without losing data or applications using the ISO file since it's a supported installation path.

However, before you upgrade to Windows 11 from Windows 8.1, you have to make sure that your laptop or desktop meets the minimum system requirements. For example, the computer must have a Trusted Platform Module 2.0 and Secure Boot present and enabled, it must also have a UEFI firmware, and the processor has to be an Intel's 8th Gen or newer or an AMD Zen 2 or newer. Original equipment manufacturers can still ship computers without a TPM 2.0 coprocessor upon Microsoft's approval. Some third-party software may refuse to run on unsupported configurations of Windows 11. The official, release version of Windows 11 is now available as a free upgrade to anyone who has Windows 10 and a PC that meets Microsoft's minimum hardware requirements.

However, the Redmond software giant isn't pushing the upgrade to every eligible system at once. Some users will be offered the option to upgrade in their Settings menu on or around the October 5th official launch date while others may be waiting until 2022. Internet Explorer has been replaced by the Chromium-based Microsoft Edge as the default web browser, and Microsoft Teams is integrated into the Windows shell.

Microsoft also announced plans to allow more flexibility in software that can be distributed via Microsoft Store, and to support Android apps on Windows 11 . If you are having a brand new laptop or PC, then your system must be compatible with Windows 11 or even might come with it preinstalled. But issues may arise with the older versions of PCs, as its hardware might not match with the requirements of Windows 11. If your PC has a 7th gen or previous Intel CPU, then it is unsupported by the latest upgrade.

Still, you can migrate to Windows 11, but the way is a little more complicated as you will need to download install files, then perform a clean install and then restore the program and data files. Once you complete the steps, the upgrade process will begin preserving your files and applications. After the installation, you won't need to complete the out-of-box experience to choose your privacy settings. At least 16GB of RAM The basic system requirements of Windows 11 differ significantly from Windows 10. Windows 11 only supports 64-bit systems such as those using an x86-64 or ARM64 processor; IA-32 processors are no longer supported. Thus, Windows 11 is the first ever consumer version of Windows not to support 32-bit processors and 16-bit software .

The minimum RAM and storage requirements were also increased; Windows 11 now requires at least 4GB of RAM and 64GB of storage. S mode is only supported for the Home edition of Windows 11. The compatibility list includes the Intel Core i7-7820HQ, a seventh-generation processor used by the Surface Studio 2, although only on devices that shipped with DCH-based drivers. In October 2019, Microsoft announced "Windows 10X", a future edition of Windows 10 designed exclusively for dual-touchscreen devices such as the then-upcoming Surface Neo.

Legacy Windows applications would also be required to run in "containers" to ensure performance and power optimization. Microsoft stated that it planned to release Windows 10X devices by the end of 2020. Citing security considerations, the system requirements for Windows 11 were increased over Windows 10. While the OS can be installed on unsupported processors, Microsoft does not guarantee the availability of updates. Windows 11 also drops support for 32-bit x86 CPUs and devices which use BIOS firmware.

You can refer to our knowledge base for a list of tested systems to determine if your device eligible to upgrade to Windows -11. Many PCs that are less than four years old will be able to upgrade to Windows 11. They must be running 20H1 or later version of Windows 10 and meet the minimum hardware requirements to receive the Windows 11 upgrade. Most Windows 10 PCs currently being sold will be able to upgrade to New Windows. For the PC to be able to upgrade to New Windows, it must meet the minimum hardware specifications and specific hardware is required for some features found here. The upgrade rollout plan is still being finalised but is scheduled to begin late in 2021 and continue into 2022.

Once you complete the steps, the tool will download the files and create an installation media, which you can then use to upgrade a compatible computer to Windows 11. If you have had the same installation for a long time, you might need to analyze and repair the current setup to fix missing or damaged files. Otherwise, during the upgrade process, the chances of running into issues will be high. However, if you plan to proceed with a clean installation using a bootable USB flash drive, then you can't skip this suggestion since the previous installation will be erased during the process. Windows 11 SE was announced on November 9, 2021, as an edition exclusively for low-end devices sold in the education market, and a successor to Windows 10 S. It is bundled with applications such as Microsoft Office for Microsoft 365, Minecraft Education Edition, and Flipgrid, while OneDrive is used to save files by default.

Windows 11 SE does not include Microsoft Store; third-party software is provisioned or installed by administrators. A redesigned user interface is present frequently throughout the operating system, building upon Fluent Design System; translucency, shadows, a new color palette, and rounded geometry are prevalent throughout the UI. With its machine learning technology, Microsoft has determined further devices on which the Windows 11 update prompt should now appear automatically. The Redmond-based software company has not revealed any additional information on which exact PC configurations are included in this third group. However, manually triggering the Windows 11 update, which is how many tech enthusiasts probably installed Windows 11 in the past weeks, is no longer necessary on these PCs. Users can simply check the regular Windows Update application in order to verify whether the Windows 11 upgrade is ready to download on their respective device.

All Dell PCs with Windows 10 currently being sold on dell.com will be able to upgrade to Windows 11. For the PC to be able to upgrade to Windows 11, it must meet the minimum hardware specifications and specific hardware is required for some features. The upgrade rollout plan is still being finalized but is scheduled to begin late in 2021 and continue into 2022. If the Microsoft Surface family of products isn't your style though, other brands like Dell, Asus and HP have all released pages online that specify what devices are Windows 11 ready. Note that many won't come with the new operating system installed, but as they all meet the minimum system requirements, you can simply buy the laptop or 2-in-1 as normal and then update it yourself.

All HUAWEI PCs with Windows 10 currently being sold on HUAWEI Consumer BG website will be able to upgrade to Windows 11. For both types of upgrades, head to Microsoft's Windows 11 download page. To perform an in-place upgrade, use the Windows 11 Installation Assistant.

For a clean install, you must create a bootable USB drive or DVD disc. Windows users should first try the Media Creation Tool for this process, since it does all the work for you. Mac and Linux users will have to flash or burn the ISO file for Windows 11 to a drive or disc, respectively. You can check out our guide on how to upgrade to Windows 11 for more details on each of these methods. After you complete the steps, the device should be able to boot from a USB installation media and pass the minimum system requirements check.

In addition to the processor, memory, and hard drive space requirements, Windows 11 needs two security features, including a Trusted Platform Module and Secure Boot, to be enabled on the Unified Extensible Firmware Interface . Furthermore, if you plan to upgrade with a clean installation, you will also need to make sure the computer can start from a USB flash drive. For example, even though Windows 11 is available as a free optional update for Windows 10, the device must meet the new system requirements. You need to ensure that the Trusted Platform Module and Secure Boot are enabled on the computer. You also need to make sure the device has enough space and there are no problems before continuing with the upgrade.

Microsoft Windows 11 Upgrade Price Furthermore, you want to create a backup in the case you need to roll back, check the activation status, and create installation media. Perhaps the most important thing to know about the release of Windows 11 is that we should expect it to change significantly over the next few years. I've been using beta versions of Windows 11 for a month in the lead-up to writing this review, and it seems like every few days there's a minor new feature or redesigned app to check out. We may not see that feature fully realized in Windows until next year. There is also the possibility that some bugs and issues may appear on Windows 11 at release. Waiting to roll out free upgrades would give Microsoft the time to address any problems before rolling out the free upgrade.

The computing giant did something similar in 2018 when it delayed its October update by a month after some users who installed the update reported losing files. Microsoft makes you accept that the company can stop providing updates, and security patches to Windows 11 on these devices. While Microsoft is unlikely to do that in practice, it's still better to be on the safer side.

Also, you're likely to run into driver incompatibility issues on unsupported devices. Especially, if your computer is running hardware that is more than 5-6 years old. As part of the minimum system requirements, Windows 11 only runs on devices with a Trusted Platform Module 2.0 security coprocessor.

According to Microsoft, the TPM 2.0 coprocessor is a "critical building block" for protection against firmware and hardware attacks. In addition, Microsoft now requires devices with Windows 11 to include virtualization-based security , hypervisor-protected code integrity , and Secure Boot built-in and enabled by default. The operating system also features hardware-enforced stack protection for supported Intel and AMD processors for protection against zero-day exploits.

Microsoft commercially released Windows 11 on Oct. 4, and noted that it's a free upgrade for Windows 10 systems that meet the new operating system's minimum requirements. Individuals with Windows 10 systems that pass Windows 11's stringent hardware requirements will be offered the new OS via the Windows Update mechanism. It'll replace the underlying Windows 10 bits with Windows 11 bits via an automated "in-place upgrade" approach. However, it's possible for users to decline the upgrade and continue with Windows 10. To see if your PC is eligible to upgrade, refer to our supported computer lists. Once you've chosen a method for your upgrade, be sure to first look over our Windows 11 upgrade checklist to get all your ducks in a row.

It'll make it easier to zip through the process—and recover faster if something happens to go awry. And while you're waiting for the installation to complete, you can check out our Windows 11 review as well as six new features you should try after you make the jump. Once you complete the steps, the package will download, and you can then use it to upgrade any computer that meets the minimum requirements. However, you will need an internet connection to proceed with the upgrade. After you complete the steps, repeat the instructions to back up the files on the remaining accounts . In addition to making a copy of your files, it's also recommended to create a list of the installed programs with their respective product keys to know what you need to reinstall in the new setup.

If you usually do not sync passwords and bookmarks with an online service, this is a good time to export your browser credentials and links. Microsoft will soon updateWindows 10 users to Windows 11, if you have computer hardware and software meeting specific prerequisite requirements. While you may be able to take steps to block the transition, technically speaking this update is not optional—it will happen as part of a normal, scheduled update. While not wanting to undermine that message, Microsoft also knows that it has users who will still want to try Windows 11 on older hardware—not least IT administrators with an office full of aging machines. With that in mind, the company told The Verge that users can install Windows 11 on unsupported devices if they want to, although this won't be mentioned in any official way.

What's more, Microsoft is being non-committal about how many updates they will provide for Windows 11 on older PCs. Windows 11 isn't perfect; it has its kinks and bugs but should you consider updating regardless of the problems? Windows 11 brings too little of an update to the table for a major generation upgrade.

Most of the system's core functionality remains the same, with only a fresh coat of paint and a few gimmicks like the widget panel. While the system does offer a better and more unified design language, Windows 11 could have easily passed as a Windows 10 update. The arbitrary system requirement limitations, in addition to very similar performance metrics to its predecessor, make it a very difficult recommendation. The OS also suffers from a lot more bugs that the company had already fixed for Windows 10. All the new features in Windows 11 feels like service updates to Windows 10. Windows 11 is a difficult recommendation in its current state, and with Windows 10's continued support till 2025, there is very little incentive to update.